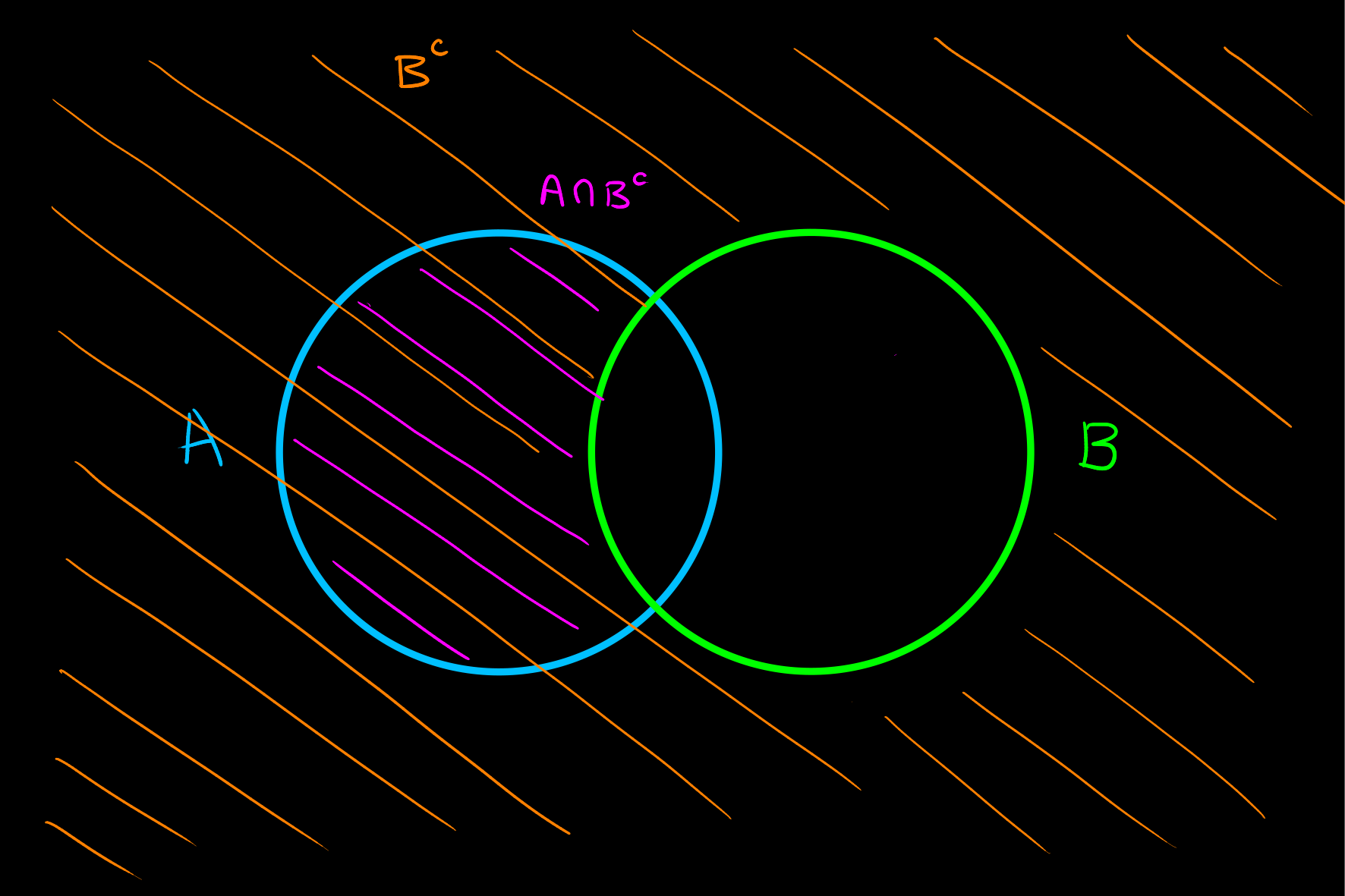
Set Difference
Definition
Given two sets \(A\) and \(B\), the set difference \(A - B\) (or \(A \setminus B\) is defined as the set of all elements which are in \(A\) but not in \(B\):
\[ A - B = \{x \in \mathcal{U} : x \in A \ \text{and} \ x \notin B\}.\]
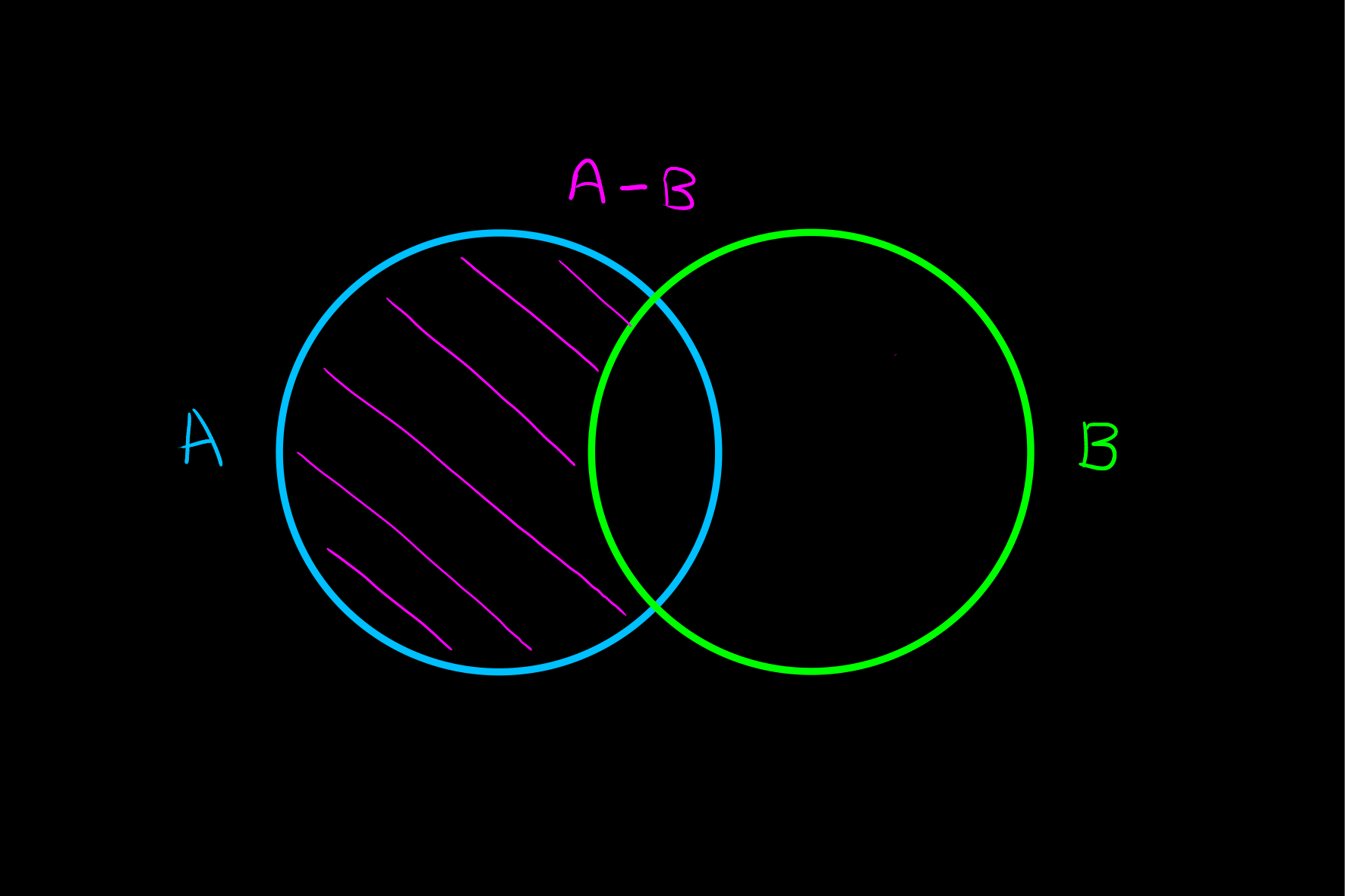
Equivalent Definitions
Theorem
The set difference can be equivalently defined by:
\[ A - B = A \cap B^{c}.\]
The proof of this fact is fairly straightforward:
\[\begin{align*}
& x \in A - B \\
\iff & x \in A \ \text{and} \ x \notin B \\
\iff & x \in A \ \text{and} \ x \in B^{c} \\
\iff & x \in A \cap B^{c}. \\
\end{align*}\]
